Why are there twelve notes?
And why did Pythagoras hate beans?
I can answer one of those two questions!
First, let’s time-travel back to Ancient Greece:
The West Loves Ratios
In the West, humanity’s search for meaning and order is wrapped up alongside the notion of beauty.
Ever heard of the Golden Ratio? Here’s some math to start your day RIGHT:
And here’s how you can visualize it with colors and shapes… ooo:
Check out this romanticization by someone smarter than I:
Some of the greatest mathematical minds of all ages, from Pythagoras and Euclid in ancient Greece, through the medieval Italian mathematician Leonardo of Pisa and the Renaissance astronomer Johannes Kepler, to present-day scientific figures have spent endless hours over this simple ratio and its properties. ... Biologists, artists, musicians, historians, architects, psychologists, and even mystics have pondered and debated the basis of its ubiquity and appeal. In fact, it is probably fair to say that the Golden Ratio has inspired thinkers of all disciplines like no other number in the history of mathematics.
— Mario Livio, astrophysicist and author of The Golden Ratio: The Story of Phi, the World's Most Astonishing Number
Nature is incredible:
Louder for the people in the back:
Counterpoint: You can put that squiggly picture over pretty much anything and claim it’s the golden ratio:
But the point isn’t whether or not the Golden Ratio is, in fact, divine. This isn’t a math post! Instead, I’m trying to share the frame of mind from which Western music was derived.
In other words: a desire for order. For reason. For divinity in the notes and the world, regardless if it’s really there.
Pythagoras and Ancient Greek Tuning
“Mr. A-squared” was a mystic-meets-mathematician, searching for the math behind beauty. He and his followers developed Greek Tuning.
Naturally, they developed their system around the overtone series.
But what are overtones? Check out a little of this example of Tuvan throat singing. The vocalist is singing a fixed low pitch and changing the shape of their mouth and throat to control overtones that appear over above the fundamental pitch. It’s like they’re singing two notes at once, one with their vocal cords the other with their mouth shape:
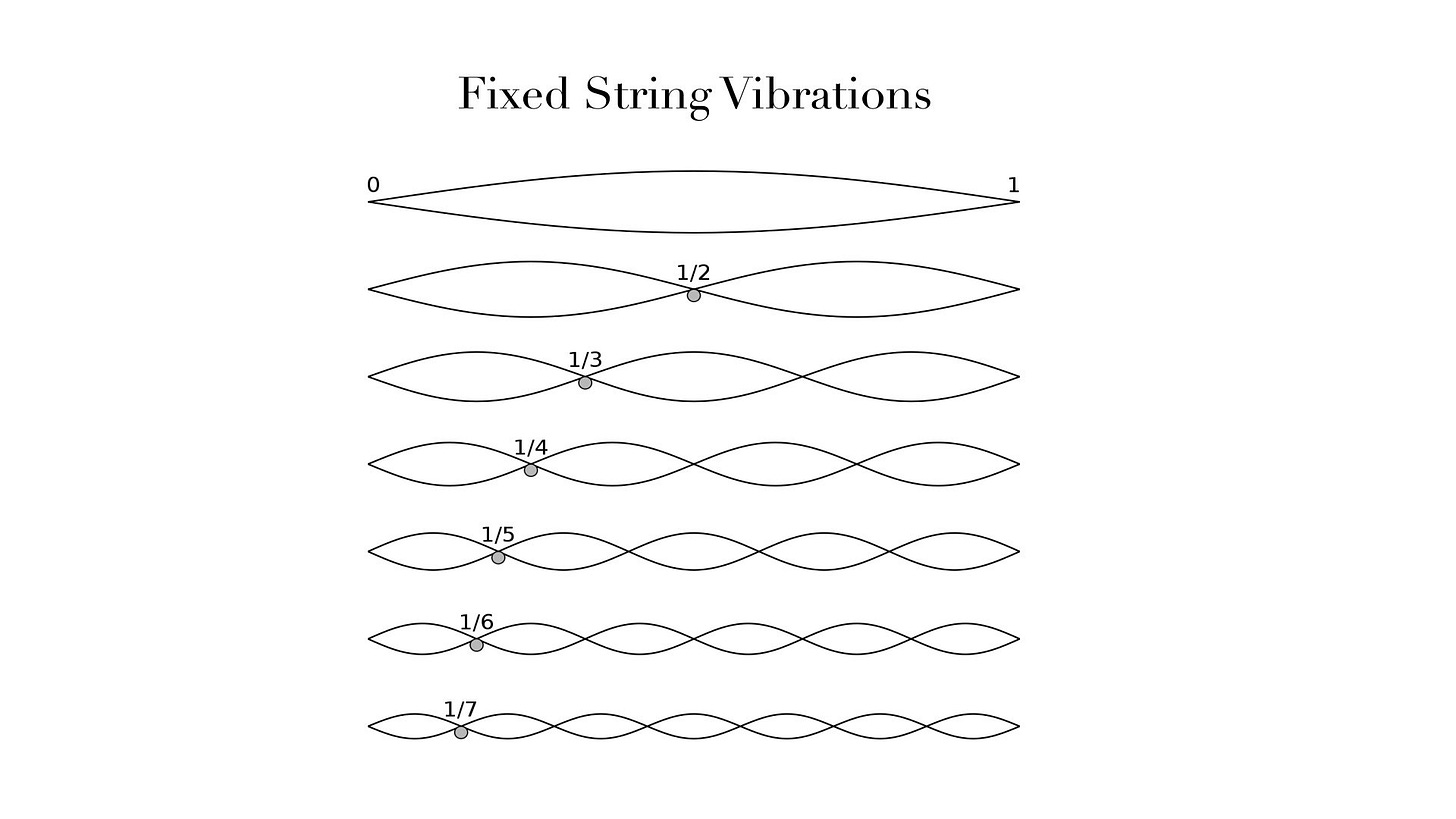
To get more technical, here’s what the overtone series looks like on a string:
Consider the oldest (pitch-based) ancient instruments. Archeologists have found simple flutes from about 50,000 years ago. Many of these early flutes would use the light, hollow bones of a bird. Holes would be drilled so the player could alter the length of the air column inside the flute with their fingers:
And here’s an example of an early lyre (kinda like a harp):
By adjusting the tension on a string (seen here at the top of the instrument), you can change how it vibrates.
The Greeks likely did not have polyphony, or harmony in the way we conceptualize it. Plato’s writings say that most Greek music consisted of single melodies without harmonies. Research suggests much of it was poetry accompanied by the lyre (above) or the aulos (I want one).
There are some fragments in Euripides' play Orestes, indicating simultaneous notes and complex rhythms. But we’re not sure how to play them, since their concept of musical notation wasn’t quite like ours:
The “Perfect” Octave (1:2 Ratio)
The octave is a truly incredible thing. I even got a bit spiritual about it in my last post.
It’s the doubling of a frequency. Any frequency. It’s what allows us to translate things like an earthquake into the range of human hearing or a bee’s wings. We octave shift up or down.
It’s also the first and strongest overtone in the harmonic series (like the Tuvan throat singers were using). So nature itself is kinda screaming about how awesome octaves are!
And here’s the key point: We perceive octaves to be the same pitch despite their difference in frequency.
That’s what allows a C to be a C regardless of how high or low it is. Middle C vibrates at 261.626 Hz in our standard, modern system.
The octave above is (261.626*2)≈523.251 Hz
Check out the repeating patterns of a keyboard. These each reflect octaves. Changes in frequency up and down but not in pitch:
The first two notes (“some” and “where”) of Somewhere Over the Rainbow are octaves. Same note. The higher note vibrates twice as fast as the first.
So We’ve Got Octaves (2:1), Let’s Add Fifths (3:2)
Expanding on this idea of perfect ratios, we add the ratio of 3:2. Between the octaves and this new ratio (the Perfect Fifth!), we can derive all 12 musical notes.
Feel free to let your eyes glaze over:
Let’s start with C.
A perfect fifth away from C, we call a G.
Let’s go all the way around. Notice how after 12 notes, it ends up back where we started:
C to G; G to D; D to A; A to E; E to B; B to F#; F# to C#; C# to G# (aka Ab, same thing in our system); Ab to Eb; Eb to Bb; Bb to F; F returns to C.
This is called the circle of fifths.
In the next post, I’ll dig deeper into the circle of fifths. It’s a daunting musical diagram, but a very powerful way to understand Western music on its own terms. I’ll break it down in a way that’s painless for musicians and nonmusicians alike!
Recommended Listening
One of my earliest pod episodes covered this same topic, but I hope this written companion gives a bit more clarity on the subject:
Thanks for reading,
Scoob